PROBABILIDAD CONDICIONAL
Consideremos una urna que contiene 4 bolillas rojas y 5 blancas. De las 4 bolillas rojas, 2
son lisas y 2 rayadas y de las 5 bolillas blancas, 4 son lisas y una sola es rayada.
Supongamos que se extrae una bolilla y, sin que la hayamos mirado, alguien nos dice que
la bolilla es roja, ¿cuál es la probabilidad de que la bolilla sea rayada?
Sean los sucesos A: “la bolilla es rayada” y B: “la bolilla es roja”. Obviamente, sin ninguna
información previa, P(A)= 3/9=1/3 y P(B)=4/9.
Sin embargo, como sabemos que la bolilla es roja, la probabilidad de que sea rayada es
½, ya que, de las rojas la mitad es lisa y la mitad rayada. Observemos, que al ocurrir B, el
espacio muestral se reduce.
En general, dado un experimento y su espacio muestral asociado, queremos determinar
cómo afecta a la probabilidad de A el hecho de saber que ha ocurrido otro evento B.
Definición: Sean A y B eventos tales que P(B) > 0, la probabilidad del evento A
condicional a la ocurrencia del evento B.
Definición: Sean A y B eventos tales que P(B) > 0, la probabilidad del evento A
condicional a la ocurrencia del evento B es
Ejemplos: 1) En el ejemplo anterior, P(B)=4/9 y
2) Consideremos una población en la que cada individuo es clasificado según dos
criterios: es o no portador de HIV y pertenece o no a cierto grupo de riesgo que
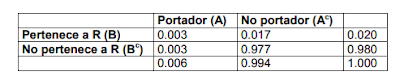
denominaremos R. La correspondiente tabla de probabilidades es:
En esta población, la probabilidad de que un individuo sea portador es P(A)=0.006 y la
probabilidad de que sea portador y pertenezca al grupo de riesgo R es P(A ∩ B)=0.003.
Dado que una persona seleccionada al azar pertenece al grupo de riesgo R, ¿cuál es la
probabilidad de que sea portador?
es decir que 150 de cada 1000 individuos del grupo de riesgo R, son “probablemente”
portadores de HIV.
Calculemos ahora la probabilidad de que una persona sea portadora de HIV, dado que no
pertenece al grupo de riesgo R.
es decir que sólo 3 de cada 1000 individuos no pertenecientes al grupo de riesgo R, son
“posibles” portadores de HIV
PROPIEDADES DE LA PROBABILIDAD CONDICIONAL
Dado un suceso B fijo tal que P(B) > 0, P(•|B)
es una probabilidad, en el sentido que satisface los axiomas de probabilidad y por lo tanto
todas las propiedades que se deducen a partir de ellos. Por ejemplo:
A1. P(A|B) ≥ 0 para todo suceso A.
A2. P(S|B) = 1.
Ejercicios: 1) Verificar que P(•|B) satisface el axioma A3a.
2) Verificar que P((A1 ∪ A2) | B) = P(A1
| B) + P(A2 | B) – P((A1 ∩ A2) | B)
Regla del producto: Dados dos sucesos A y B, tales que P(B) > 0,
P(A ∩ B) = P(A|B) P(B)
Si además, P(A) > 0,
P(A ∩ B) = P(B | A) P(A)
Ejemplo: En el ejemplo presentado al comienzo, supongamos ahora que se extraen dos
bolillas sin reposición . ¿Cuál es la probabilidad de extraer una bolilla roja y una blanca,
en ese orden?
Sean C: “la primera bolilla es roja” y D: “la segunda bolilla es blanca”. debemos calcular
P(C ∩ D). Aplicando la regla del producto
La regla del producto es especialmente útil cuando el experimento consta de varias
etapas ya que se puede generalizar. Así, por ejemplo, si P(A1 ) > 0 y P(A1 ∩ A2 ) > 0 , se
tiene
P A1 ∩ A2 ∩ A3 = P (A1 P A2 A1 P A3) A1 ∩ A2
y se extiende a n sucesos.
Ejemplo: En el mismo ejemplo, ¿cómo podemos obtener la probabilidad de que la
segunda bolilla extraída sea blanca (suceso D)?. Sabemos calcular, usando la regla del
producto la probabilidad de que la segunda sea blanca y la primera sea roja. Hemos visto
que esta probabilidad es P(C ∩ D) = 5 18. Del mismo modo podemos obtener la
probabilidad de que ambas bolillas sean blancas (suceso (D ∩ C c)). Esta probabilidad es
¿Cómo podemos obtener ahora la probabilidad de que la primera bolilla haya sido roja
(suceso C) sabiendo que la segunda fue blanca (suceso D)? La probabilidad requerida es.
Los resultados (1) y (2) son ejemplos de aplicación de los dos Teoremas que veremos a
continuación: el Teorema de la Probabilidad Total y el Teorema de Bayes,
respectivamente.
Definición: Una colección de eventos A A Ak , ,..., 1 2 constituye una partición del espacio
muestral S si
1. Ai ∩ Aj = ∅ ∀ i ≠ j
2. P A i ( i ) > 0 ∀
TEORBAYESEMA DE BAYES
Sea A A Ak , ,..., 1 2 una partición del espacio muestral S y sea B un
suceso cualquiera tal que P(B) > 0,
Dem:
En el numerador se aplicó la regla del producto y en el denominador el Teorema de la
probabilidad total.
El Teorema de Bayes describe cómo es posible “revisar” la probabilidad inicial de un
evento o probabilidad a priori (P(Ai
)) para reflejar la información adicional que nos provee
la ocurrencia de un evento relacionado. La probabilidad revisada se denomina
probabilidad a posteriori
Ejemplo: Supongamos que cierta prueba para detectar la presencia de una enfermedad
en un individuo, da resultado positivo (detecta la presencia de la enfermedad) en un
individuo enfermo con probabilidad 0.99 y en un individuo sano con probabilidad 0.02
(falso positivo). Por lo tanto, dicha prueba no detecta la enfermedad en un individuo sano
con probabilidad 0.98 y no la detecta en un individuo enfermo con probabilidad 0.01 (falso
negativo). Es decir que si denotamos A: “la persona padece esa enfermedad” y B: “la
prueba es positiva”,.
Se supone, en base a estudios previos, que la incidencia de esa enfermedad en cierta
población es 0.001, es decir que la probabilidad a priori de A es 0.001. Se selecciona al
azar un individuo de esa población, se le aplica la prueba y el resultado es positivo, ¿cuál
es la probabilidad de que en efecto padezca la enfermedad?
Debemos calcular la probabilidad a posteriori de A, P(A|B):
Por lo tanto, la probabilidad de que esté enfermo, habiendo sido positivo el resultado de la
prueba es aproximadamente 0.05.
Las probabilidades a posteriori dependen fuertemente de las probabilidades a priori. Si se
aplica la prueba a individuos de una población en la cual la incidencia de la enfermedad
es mucho mayor, también aumentará la probabilidad a posteriori.
Verifique ésto, suponiendo ahora que P(A) = 0.01.
Más adelante, desarrollaremos otro ejemplo de aplicación de estos Teoremas.
INDEPENDENCIA
La definición de probabilidad condicional nos permite “revisar” la probabilidad P(A)
asignada a un suceso, cuando se sabe que otro suceso B ha ocurrido. Hay casos en los
que P(A | B) ≠ P(A), mientras que en otros P(A | B) = P(A), es decir que la ocurrencia del
suceso B no altera la probabilidad de ocurrencia de A.
Ejemplo: De una urna que contiene 4 bolillas negras y 6 blancas se extraen dos bolillas
sin reposición , ¿cuál es la probabilidad de que la segunda bolilla sea blanca, sabiendo
que la primera es negra?
Denominando A: “la segunda bolilla es blanca” y B: ”la primera bolilla es negra”,
y, por lo tanto, P(A| B) ≠ P(A), es decir que la ocurrencia del suceso B modifica la
probabilidad del suceso A
Observemos que la probabilidad de que la segunda bolilla sea blanca coincide con la
probabilidad de que la primera lo sea.
Ejercicio: Verificar que, en cambio, si las extracciones se realizan con reposición, P(A) =
P(A|B).
Diremos que los eventos A y B son independientes si la información acerca de la
ocurrencia o no de uno de ellos no afecta la probabilidad de ocurrencia del otro,
Definición: Los eventos A y B son independientes si
P(A ∩ B) = P(A) P(B)
Si la igualdad no se cumple, decimos que A y B son dependientes
Proposición: Supongamos P(B) > 0, A y B son independientes si y sólo si P(A|B)=P(A).
⇐) Aplicando la regla del producto, si P(B)>0, P(A ∩ B) = P(A| B)P(B) = P(A)P(B).
Observación: Si P(B) = 0, como A ∩ B ⊆ B , P(A ∩ B) = 0, y por lo tanto la igualdad
P(A ∩ B) = P(A)P(B) siempre se satisface.
Ejemplo: De un mazo de 40 cartas españolas, se extrae una carta al azar. Consideremos
los siguientes sucesos:
A: "a carta es copa o espada”
B: “ la carta no es copa”
C: “la carta es copa u oro”
Propiedades: 1) Si los sucesos A y B son excluyentes, es decir si A ∩ B = ∅ y si P(A)>0,
P(B) > 0, entonces A y B no son independientes.
Dem: En efecto, en este caso, 0 = P(A ∩ B) ≠ P(A)P(B).
2) Si P(B) = 0, entonces B es independiente de cualquier suceso A tal que P(A) > 0
Dem: Como A ∩ B ⊆ B, P(A ∩ B) = 0 y por lo tanto P(A ∩ B) = P(A) P(B), es decir que A y
B son independientes.
3) Si A ⊆ B, P(A) > 0 y P(B) <1, A y B no son independientes
Dem: Como A ⊆ B ⇒ A ∩ B = A⇒ P(A ∩ B) = P(A) ≠ P(A)P(B). Luego, A y B no son
independientes.
4) Si A y B son sucesos independientes, A y Bc
también lo son.
Dem:
P(A) = P(A ∩ B) + P(A ∩ B ) ⇒ P(A ∩ B ) = P(A) − P(A ∩ B) = P(A) − P(A)P(B) = c c
( ) ( ) 1 ( ) ( ) ( )
c P A − P B = P A P B .
DEPENDIENTES
Dos o más eventos serán dependientes cuando la ocurrencia o no-ocurrencia de uno de ellos afecta la probabilidad de ocurrencia del otro (o otros). Cuando tenemos este caso, empleamos entonces, el concepto de probabilidad condicional para denominar la probabilidad del evento relacionado. La expresión P(A|B) indica la probabilidad de ocurrencia del evento A sí el evento B ya ocurrió.
Se debe tener claro que A|B no es una fracción.
P(A|B) = P(A y B)/P(B) o P(B|A) = P(A y B)/P(A)
Ejemplos:
Una caja contiene 4 canicas rojas, 3 canicas verdes y 2 canicas azules. Una canica es eliminada de la caja y no es reemplazada. Otra canica se saca de la caja. Cuál es la probabilidad de que la primera canica sea azul y la segunda canica sea verde?
Ya que la primera canica no es reemplazada, el tamaño del espacio muestral para la primera canica (9) es cambiado para la segunda canica (8) así los eventos son dependientes.
P(azul luego verde) = P(azul) · P(verde)
TEOREMA DE PROBABILIDAD TOTAL
Una vez expuesta definición de probabilidad condicional y tener clara su aplicación se da inicio al estudio del Teorema o regla de Probabilidad Total. Pero previamente se debe conocer una definición fundamental para su aplicación y fundamentación teórica, y no es otra que la de partición.
Definición: sea el espacio muestral Ω un conjunto no vacío, se define como partición de Ω a cualquier familia {B}i=1 de subconjuntos de Ω que sean mutuamente excluyentes y totalmente exhaustivos. Esto quiere decir que una partición se cumple cuando
reúne las condiciones siguientes:
i. Bi ∩ Bj = Vacío para todo i ≠ j La intersección entre los subconjuntos es vacía
ii. B1UB2U . . . UBn = Ω La unión de todos los subconjuntos resultado Ω
Así por ejemplo si Ω = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} entonces {(1, 2, 3) ; (4, 5, 6, 7) ; (8, 9, 10)} son una partición de Ω
El teorema o regla de probabilidad total indica cómo calcular la probabilidad de un suceso o evento A cuando se conocen las probabilidades condicionales de P(A/Bi) donde las Bi forma una partición del espacio muestral Ω.
Veamos un ejemplo de esta situación antes de pasar a enunciar el Teorema de Probabilidad Total.
Ejemplo de ejercicio aplicando Probabilidad Total
Supóngase que se tiene una población de 50 trabajadores discriminados en Empleados Administrativos y Personal Operativo los cuales laboran en tres departamentos distintos. Departamento de Producción, Departamento de Acabado y Departamento de Mantenimiento.
Los cuales se discriminan de la siguiente manera:
:
Si se selecciona un trabajador de esta empresa en forma aleatoria, ¿Cuál es la probabilidad de que sea Personal Administrativo?
Como se puede observar, al realizar la unión de los trabajadores de cada departamento se obtiene el Universo o Marco Muestral Ω y la intersección es el vacío. Y como aún no contamos con el conocimiento teórico para realizar el cálculo de dicha probabilidad. Se pasará a definir y demostrar elTeorema de Probabilidad Total
Supongamos que la familia de subconjuntos {B}i=1 es una partición de un espacio muestral Ω. Si A es un suceso de Ω entonces:
P(A) = P(A/B1)P(B1) + P(A/B2)P(B2)+ . . . +P(A/Bn)P(Bn) = 
Demostración de Teorema de Probabilidad Total
Partiendo de la identidad: A = A∩Ω
Como es una partición de Ω se tiene que:
A = A∩(B1UB2U . . . UBn)
Aplicando propiedad distributiva de la intersección con respecto a la unión se tiene que
A = (A∩B1)U(A∩B2)U . . . . U(A∩Bn)
Entonces: P(A) = P((A∩B1)U(A∩B2)U . . . . U(A∩Bn))
Por ser una partición, los (A∩Bi) son mutuamente independientes, por lo tanto
P(A) = P(A∩B1)+P(A∩B2)+ . . . . +P(A∩Bn)
Por propiedad de probabilidad condicional P(A∩Bi) = P(A/Bi)P(Bi)
Finalmente:
P(A) = P(A/B1)P(B1) + P(A/B2)P(B2)+ . . . +P(A/Bn)P(Bn) = 
Con este resultado teórico se puede resolver el ejemplo de los trabajadores:
A = Administrativo: 15
B1 = Departamento Producción: 25
B2 = Departamento de Acabado: 14
B3 = Departamento de Mantenimiento: 11
P(A) = P(A/B1)P(B1) + P(A/B2)P(B2) + P(A/B3)P(B3)
P(A) = (7/25)x(25/50) + (5/14)x(14/50) + (3/11)x(11/50)
P(A) = 0,14 + 0,1 + 0,0,6 = 0,30
EJERCICIOS RESUELTOS
PROBABILIDAD CONDICIONADA,SUCESOS INDEPENDIENTES,DEPENDIENTES,TEORÍA DE BAYES,PROBABILIDAD TOTAL.
Ejercicios Resueltos Prob. Total y Teorema de Bayes
EJEMPLO 1
En la sala de pediatría de un hospital, el 60% de los pacientes son niñas. De los niños el 35% son menores de 24 meses. El 20% de las niñas tienen menos de 24 meses. Un pediatra que ingresa a la sala selecciona un infante al azar.
a. Determine el valor de la probabilidad de que sea menor de 24 meses.
b. Si el infante resulta ser menor de 24 meses. Determine la probabilidad que sea una niña.
SOLUCIÓN:
Se definen los sucesos:
Suceso H: seleccionar una niña.
Suceso V: seleccionar un niño.
Suceso M: infante menor de 24 meses.
En los ejercicios de probabilidad total y teorema de bayes, es importante identificar los sucesos que forman la población y cuál es la característica que tienen en común dichos sucesos. Estos serán los sucesos condicionados.
a. En este caso, la población es de los infantes. Y la característica en común es que sean menores de 24 meses. Por lo tanto, la probabilidad de seleccionar un infante menor de 24 meses es un ejemplo de probabilidad total. Su probabilidad será:
b. Para identificar cuando en un ejercicio se hace referencia al teorema de bayes, hay que partir de reconocer esta es una probabilidad condicionada y que la característica común de los sucesos condicionantes ya ha ocurrido. Entonces, la probabilidad de que sea niña una infante menor de 24 meses será:
EJEMPLO 2
Un médico cirujano se especializa en cirugías estéticas. Entre sus pacientes, el 20% se realizan correcciones faciales, un 35% implantes mamarios y el restante en otras cirugías correctivas. Se sabe además, que son de genero masculino el 25% de los que se realizan correcciones faciales, 15% implantes mamarios y 40% otras cirugías correctivas. Si se selecciona un paciente al azar, determine:
a. Determine la probabilidad de que sea de género masculino
b. Si resulta que es de género masculino, determine la probabilidad que se haya realizado una cirugía de implantes mamarios.
SOLUCIÓN:
Se definen los sucesos:
Suceso F: pacientes que se realizan cirugías faciales
Suceso M: pacientes que se realizan implantes mamarios
Suceso O: pacientes que se realizan otras cirugías correctivas
Suceso H: pacientes de género masculino
a. La probabilidad de que sea de género masculino se refiere a un problema de probabilidad total, ya que es el suceso condicionado y las cirugías los condicionantes. Dicho valor será:
b. Como el suceso condicionado ha ocurrido entonces se aplica el teorema de bayes, luego, el valor de la probabilidad será:
EJEMPLO 3
Un Doctor dispone de tres equipos electrónicos para realizar ecosonogramas. El uso que le da a cada equipo es de 25% al primero, 35% el segundo en y 40% el tercero. Se sabe que los aparatos tienen probabilidades de error de 1%, 2% y 3% respectivamente. Un paciente busca el resultado de una ecografía y observa que tiene un error. Determine la probabilidad de que se ha usado el primer aparato.
SOLUCIÓN:
Se definen los sucesos:
Suceso P: seleccionar el primer aparato
Suceso S: seleccionar el segundo aparato
Suceso T: seleccionar el tercer aparato
Suceso E: seleccionar un resultado con error
Se puede observar que la pregunta es sobre determinar la probabilidad de que un examen errado sea del primer aparato, es decir, ya ha ocurrido el error. Por lo tanto, debemos recurrir al teorema de bayes. Claro está, que es necesario de igual forma obtener la probabilidad de que los aparatos produzcan un resultado erróneo, por lo tanto:
PROBABILIDAD CONDICIONADA
De una baraja de 48 cartas se extrae simultáneamente dos de ellas. Calcular la probabilidad de que:
Soluciones:











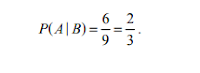








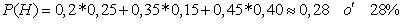
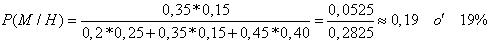
























No hay comentarios:
Publicar un comentario